Introduction
Artificial Intelligence (AI) is constantly evolving and reaching new milestones. A remarkable example is the recent publication from Google DeepMind. The new AI models AlphaProof and AlphaGeometry 2 have solved complex mathematical problems at the level of the International Mathematical Olympiad (IMO), achieving performance equivalent to a silver medalist. This achievement demonstrates the immense potential of Artificial General Intelligence (AGI) in science and technology.
Background of the International Mathematical Olympiad
The IMO has been the oldest and most prestigious competition for young mathematicians since 1959. Every year, highly talented students from around the world participate and try to solve six extremely difficult problems in algebra, combinatorics, geometry, and number theory. Many later Fields Medal winners participated in the IMO in their youth.
In recent years, the IMO has also established itself as a significant challenge in the field of machine learning. It serves as a benchmark for the advanced mathematical capabilities of AI systems.
The Innovations: AlphaProof and AlphaGeometry 2
AlphaProof: A Formal Approach to Proof
AlphaProof is a new system based on Reinforcement Learning that can prove mathematical statements in the formal language Lean. It combines a pre-trained language model with the AlphaZero algorithm, which previously mastered chess, shogi, and Go. The advantage of formal languages is that proofs can be formally verified. However, their application in machine learning was previously limited by the limited amount of human-written data.
AlphaProof bridges this gap by translating natural language problems into formal statements and creating an extensive library of formal problems. The system generates solution candidates and proves or disproves them by searching for possible proof steps in Lean. During training for the IMO, AlphaProof proved or disproved millions of problems to improve its capabilities.
AlphaGeometry 2: A More Competitive Approach
AlphaGeometry 2 is an improved version of the original AlphaGeometry system. It’s a neuro-symbolic hybrid system based on the Gemini model and trained with a much larger amount of synthetic data. These improvements enable the model to solve more challenging geometry problems.
AlphaGeometry 2 uses a symbolic engine that is significantly faster than its predecessor. The system solved one of the IMO 2024 problems within just 19 seconds of receiving the formalization.
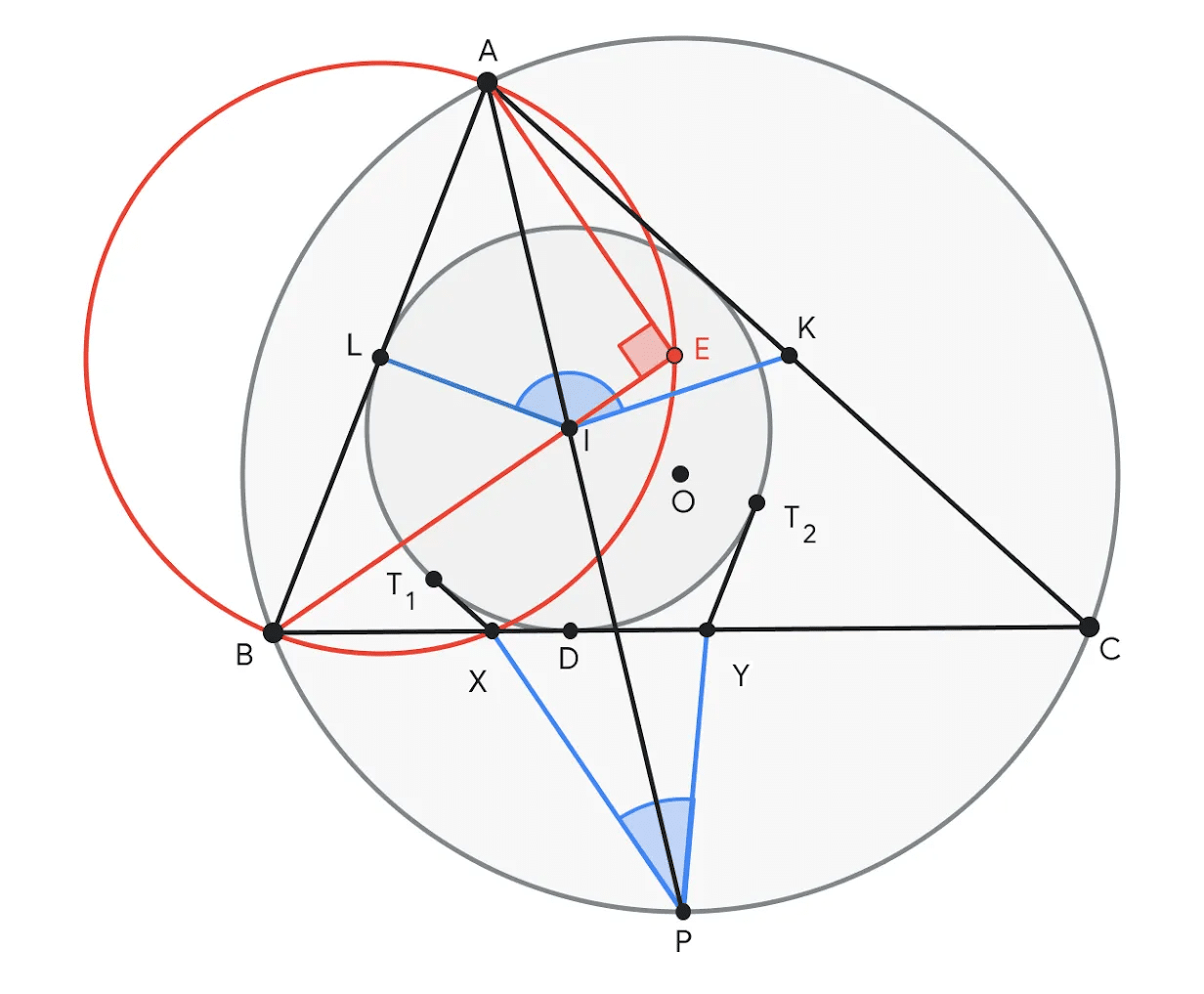
Problem 4 of the IMO
Illustration of Problem 4, where it must be proved that the sum of ∠KIL and ∠XPY equals 180°. AlphaGeometry 2 suggested constructing E, a point on line BI, such that ∠AEB = 90°. Point E helps determine the midpoint L of AB, creating many pairs of similar triangles like ABE ~ YBI and ALE ~ IPC required for proving the conclusion.
Performance Evaluation and Results
This year, AlphaProof and AlphaGeometry 2 were applied to the IMO problems. Solutions were evaluated by prominent mathematicians including Prof Sir Timothy Gowers and Dr Joseph Myers. AlphaProof solved two algebra problems and one number theory problem, proving the answers were correct. AlphaGeometry 2 proved the geometry problem, while both combinatorics problems remained unsolved.
Overall, the combined AI system achieved 28 out of 42 possible points, corresponding to the upper limit of the silver medal category. The system nearly reached the gold medal threshold, which begins at 29 points.
New Horizons in Mathematical Research
The developments of AlphaProof and AlphaGeometry 2 open new possibilities for collaboration between mathematicians and AI systems. In the future, mathematicians could use AI tools to explore hypotheses, try new approaches to solving long-standing problems, and complete time-consuming proof steps more quickly.
DeepMind plans to publish more technical details about AlphaProof and continues to explore various AI approaches to advance mathematical proof.
Conclusion
Google DeepMind’s advances in developing AlphaProof and AlphaGeometry 2 mark a significant step in AI research. These systems have shown that AI is capable of solving highly complex mathematical problems at a level comparable to human top performance. This could have far-reaching implications for scientific research and the application of AI in various fields.

